3.1. Convolutional Neural Networks over MLP#

Convolutional Neural Networks (ConvNets or CNNs in short) are a subset of Neural Networks that have proven very effective in areas such as image recognition and classification like image below shows an example of CNN being used for recognizing everyday objects, humans and animals.

In order to understand why Convolutional Neural Networks were required when we already had MLP models (which can represent almost any function in real world), we first have to understand how image data is represented.

Image data#

Image data is represented as a two-dimensional grid of pixels, be it a grayscale image (black and white) or a colored image. To keep it simple, let’s take a small black and white image of an 8, with square dimensions of 28 pixels (source).

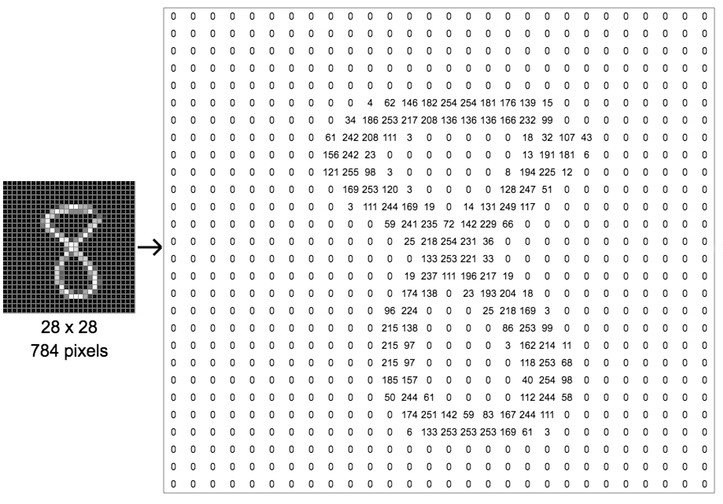
An image from a standard digital camera will have three channels – red, green and blue (RGB) – one can imagine those as three 2d-matrices stacked over each other (one for each color), each having pixel values in the range 0 to 255 (check figure below). Each such number corresponds to the brightness of a single pixel. In black-and-white images we only need one 2D matrix instead of three 2D matrices.

Till now, when dealing with MLP models, we have not considered this rich structure of the image data as input and we have considered them just as a 1D flat vector. This way we broke any spatial relationship that might exist between different pixels which is truly inappropriate.

So, in order to solve this problem CNN’s were developed. The primary purpose of Convolution in case of a CNN model is to extract complex features from the input image.

Also, later we will see that the number of trainable parameters required to train a same set of images reduce drastically in case of CNNs as compared to the MLP models. This is also another advantage of CNNs over MLP models.

Note

Convolution preserves the spatial relationship between pixels by learning image features using small squares of input data.

We will now go into the mathematical details of Convolution and will try to understand how it works over images in the upcoming sections.