3.2.2 Forward Propagation Convolution layer (Vectorized)
Contents
3.2.2 Forward Propagation Convolution layer (Vectorized)#
Now let us write (step by step) most general vectorized code using numpy (no loops will be used) to perform forward propagation on the convolution layer.
Note: The theoretical aspect of forward propagation along with the notations used can be found in the previous section (link to previous section).
Padding and Convolution functions#
We know that the input will first be padded with zeros (based on type of padding) on the edges and then it will be sent further for convolution. We will create a function to perform padding and convolutions both of which will take following parameters: input \(X\), Kernel \(K\), stride \(s\) and padding type \(p\) which can be a string (“valid” or “same”) or an integer as described in the notations (link to previous section)
Simple Input (no channels and batch)#
We will start with a simple Input (with no channels and batch) of shape \((N_h, N_w)\) and then progress further.
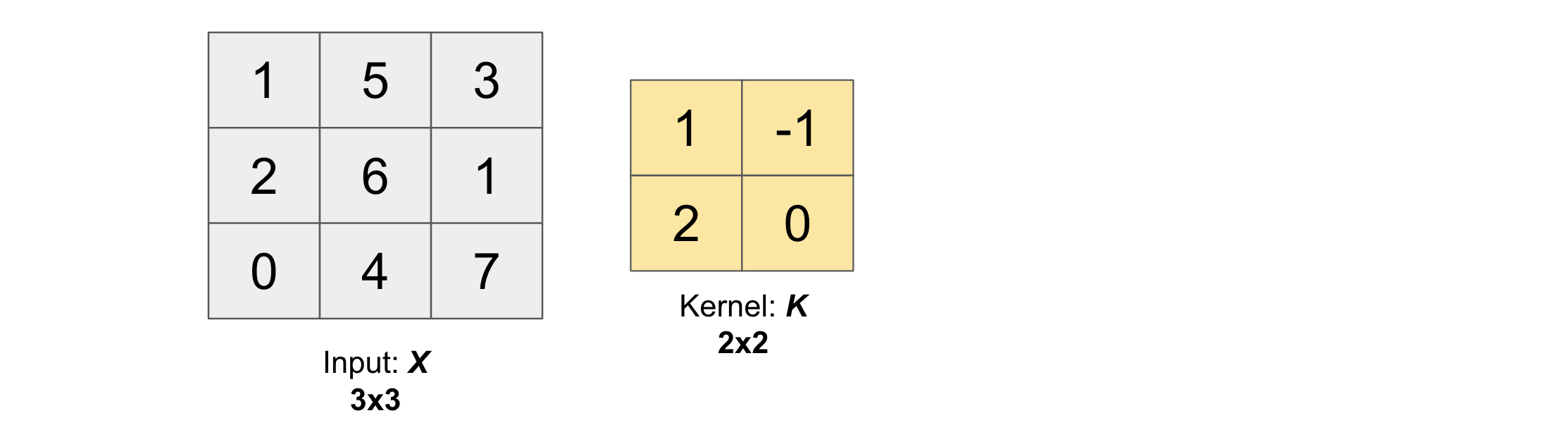
The function pad_input2D(X,K,s,p) performs padding on input \(X\) (with no channels and batch) and returns the padded matrix.
def pad_input2D(X, K, s, p='valid'):
if type(p)==int:
Nh, Nw = X.shape
pt, pb = p, p
pl, pr = p, p
elif p=='valid':
Nh, Nw = X.shape
pt, pb = 0, 0
pl, pr = 0, 0
elif p=='same':
Nh, Nw = X.shape
Kh, Kw = K.shape
sh, sw = s
ph = (sh-1)*Nh + Kh - sh
pw = (sw-1)*Nw + Kw - sw
pt, pb = ph//2, (ph+1)//2
pl, pr = pw//2, (pw+1)//2
else:
raise ValueError("Incorrect padding type. Allowed types are only 'same' or 'valid' or an integer.")
Xp = np.vstack((np.zeros((pt, Nw)), X))
Xp = np.vstack((Xp, np.zeros((pb, Nw))))
Xp = np.hstack((np.zeros((Nh+pt+pb, pl)), Xp))
Xp = np.hstack((Xp, np.zeros((Nh+pt+pb, pr))))
return Xp
Test p="valid"
import numpy as np
np.random.seed(10)
X = np.array([[1, 5, 3],
[2, 6, 1],
[0, 4, 7]])
K = np.array([[1, -1],
[2, 0]])
s = (2,2) # strides along height and width
print('X = \n\n', X, '\n')
Xp = pad_input2D(X, K, s, p='valid')
print('Xp = \n\n', Xp)
X =
[[1 5 3]
[2 6 1]
[0 4 7]]
Xp =
[[1. 5. 3.]
[2. 6. 1.]
[0. 4. 7.]]
Test p="same", stride \(s=(2,2)\)
import numpy as np
np.random.seed(10)
X = np.array([[1, 5, 3],
[2, 6, 1],
[0, 4, 7]])
K = np.array([[1, -1],
[2, 0]])
s = (2,2) # strides along height and width
print('X = \n\n', X, '\n')
Xp = pad_input2D(X, K, s, p='same')
print('Xp = \n\n', Xp)
X =
[[1 5 3]
[2 6 1]
[0 4 7]]
Xp =
[[0. 0. 0. 0. 0. 0.]
[0. 1. 5. 3. 0. 0.]
[0. 2. 6. 1. 0. 0.]
[0. 0. 4. 7. 0. 0.]
[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]]
We see that the right and bottom of the input is padded.
Test the value of \(p\) as integer (\(p=2\))
import numpy as np
np.random.seed(10)
X = np.array([[1, 5, 3],
[2, 6, 1],
[0, 4, 7]])
K = np.array([[1, -1],
[2, 0]])
s = (2,2) # strides along height and width
print('X = \n\n', X, '\n')
Xp = pad_input2D(X, K, s, p=2)
print('Xp = \n\n', Xp)
X =
[[1 5 3]
[2 6 1]
[0 4 7]]
Xp =
[[0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0.]
[0. 0. 1. 5. 3. 0. 0.]
[0. 0. 2. 6. 1. 0. 0.]
[0. 0. 0. 4. 7. 0. 0.]
[0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0.]]
Convolution 2D
Now the function conv2d(X,K,s,p) performs convolution between input \(X\) (with no channels and batch) and Kernel \(K\) and returns the convolved matrix \(Z\) (Output).
Note: Although the operation performed is cross-correlation (link to previous chapter) and not convolution, but we will refer it to as convolution because there is no difference between cross-correlation and convolution except the fact that the kernel \(K\) is rotated by 180 degrees during convolution.
References for you
If you have problem understanding
as_strided()function of numpy (used for conv2d) please go through this link. It will give you outstanding exercises with explainations to solutions (for 1D array to 4D tensors).If you have problem understanding
einsum()function of numpy (used for conv2d) please go through this stackoverflow question.
def conv2d(X, K, s=(1,1), p='valid'):
# padding
Xp = pad_input2D(X, K, s, p=p)
print('Xp = \n\n', Xp, '\n')
Nh, Nw = Xp.shape
Kh, Kw = K.shape
sh, sw = s # strides along height and width
Oh = (Nh-Kh)//sh + 1
Ow = (Nw-Kw)//sw + 1
strides = (sh*Nw, sw, Nw, 1)
strides = tuple(i * Xp.itemsize for i in strides)
subM = np.lib.stride_tricks.as_strided(Xp, shape=(Oh, Ow, Kh, Kw),
strides=strides)
return np.einsum('kl,ijkl->ij', K, subM)
Test on p="valid"
import numpy as np
np.random.seed(10)
X = np.array([[1, 5, 3],
[2, 6, 1],
[0, 4, 7]])
K = np.array([[1, -1],
[2, 0]])
s = (1,1) # strides along height and width
print('X = \n\n', X, '\n')
print('K = \n\n', K, '\n')
Z = conv2d(X, K, s, p='valid')
print('Z = \n\n', Z)
X =
[[1 5 3]
[2 6 1]
[0 4 7]]
K =
[[ 1 -1]
[ 2 0]]
Xp =
[[1. 5. 3.]
[2. 6. 1.]
[0. 4. 7.]]
Z =
[[ 0. 14.]
[-4. 13.]]
Yay! We have obtained the same output as the one we found numerically here.
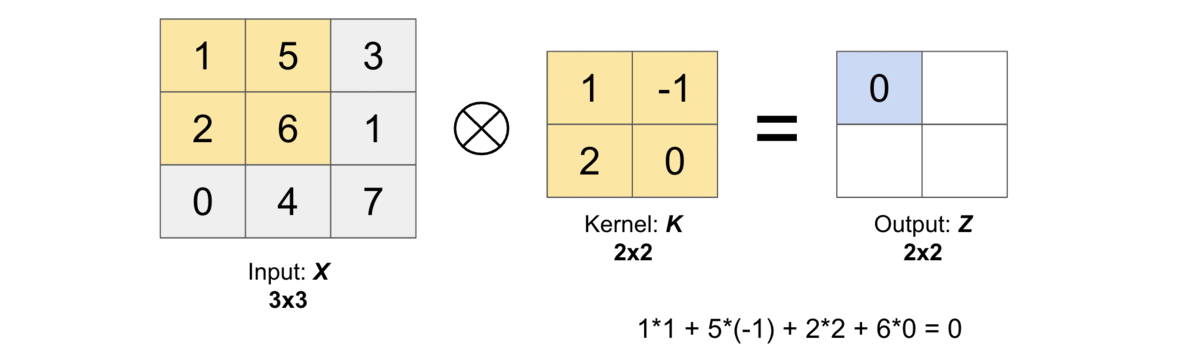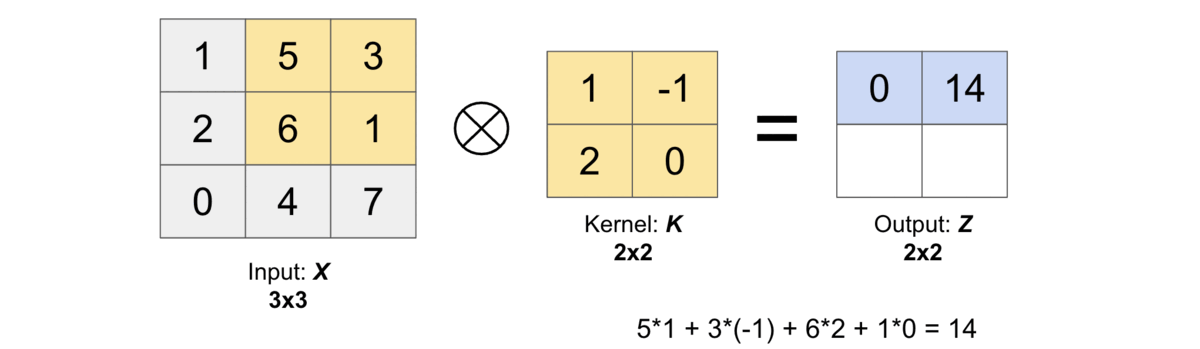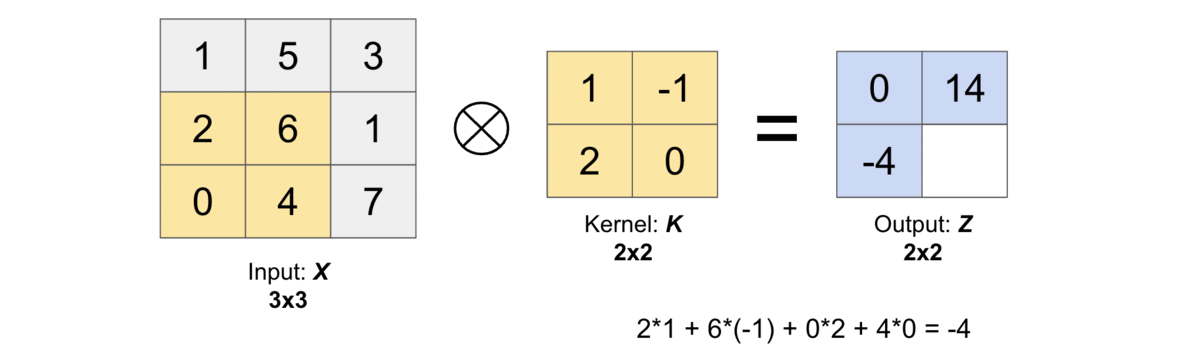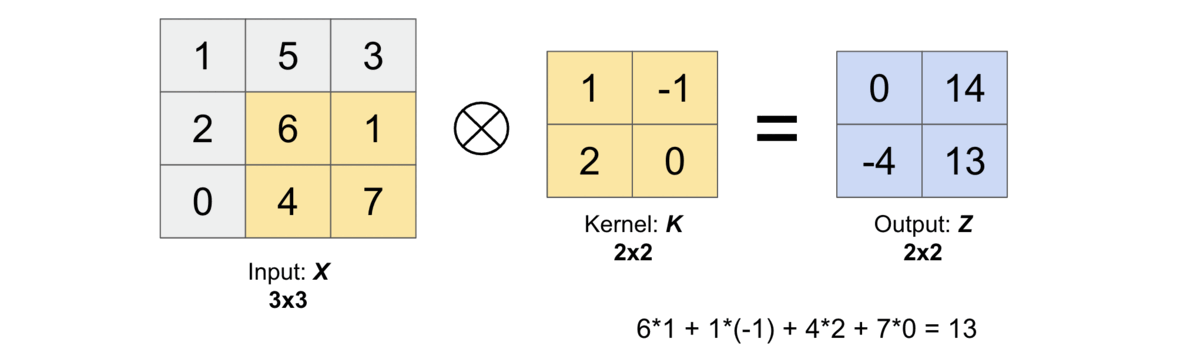
Test with p="same"
import numpy as np
np.random.seed(10)
X = np.array([[1, 5, 3],
[2, 6, 1],
[0, 4, 7]])
K = np.array([[1, -1],
[2, 0]])
s = (2,1) # strides along height and width
print('X = \n\n', X, '\n')
print('K = \n\n', K, '\n')
Z = conv2d(X, K, s, p='same')
print('Z = \n\n', Z)
X =
[[1 5 3]
[2 6 1]
[0 4 7]]
K =
[[ 1 -1]
[ 2 0]]
Xp =
[[0. 0. 0. 0.]
[1. 5. 3. 0.]
[2. 6. 1. 0.]
[0. 4. 7. 0.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]]
Z =
[[ 2. 10. 6.]
[-4. 13. 15.]
[ 0. 0. 0.]]
Input with batch of images (no channels)#
Next we will include a batch of images as Input
A batch of images as input of shape \((m, N_h, N_w)\) is used (no channels are added yet).

The function pad_input2D_batch(X,K,s,p) performs padding on input \(X\) (with no channels) and returns the padded matrix.
def pad_input2D_batch(X, K, s, p='valid'):
if type(p)==int:
m, Nh, Nw = X.shape
pt, pb = p, p
pl, pr = p, p
elif p=='valid':
m, Nh, Nw = X.shape
pt, pb = 0, 0
pl, pr = 0, 0
elif p=='same':
m, Nh, Nw = X.shape
Kh, Kw = K.shape
sh, sw = s
ph = (sh-1)*Nh + Kh - sh
pw = (sw-1)*Nw + Kw - sw
pt, pb = ph//2, (ph+1)//2
pl, pr = pw//2, (pw+1)//2
else:
raise ValueError("Incorrect padding type. Allowed types are only 'same' or 'valid' or an integer.")
zeros_r = np.zeros((m, Nh, pr))
zeros_l = np.zeros((m, Nh, pl))
zeros_t = np.zeros((m, pt, Nw+pl+pr))
zeros_b = np.zeros((m, pb, Nw+pl+pr))
Xp = np.concatenate((X, zeros_r), axis=2)
Xp = np.concatenate((zeros_l, Xp), axis=2)
Xp = np.concatenate((zeros_t, Xp), axis=1)
Xp = np.concatenate((Xp, zeros_b), axis=1)
return Xp
Test p="valid"
import numpy as np
np.random.seed(10)
X = np.random.randint(0,10, size=(2,3,3))
X[0,:,:] = np.array([[1, 5, 3],
[2, 6, 1],
[0, 4, 7]])
K = np.array([[1, -1],
[2, 0]])
s = (2,2) # strides along height and width
print('X = \n\n', X, '\n')
Xp = pad_input2D_batch(X, K, s, p='valid')
print('Xp = \n\n', Xp)
X =
[[[1 5 3]
[2 6 1]
[0 4 7]]
[[0 8 6]
[4 3 0]
[4 6 8]]]
Xp =
[[[1. 5. 3.]
[2. 6. 1.]
[0. 4. 7.]]
[[0. 8. 6.]
[4. 3. 0.]
[4. 6. 8.]]]
Test p="same", stride \(s=(1,2)\)
import numpy as np
np.random.seed(10)
X = np.random.randint(0,10, size=(2,3,3))
X[0,:,:] = np.array([[1, 5, 3],
[2, 6, 1],
[0, 4, 7]])
K = np.array([[1, -1],
[2, 0]])
s = (1,2) # strides along height and width
print('X = \n\n', X, '\n')
Xp = pad_input2D_batch(X, K, s, p='same')
print('Xp = \n\n', Xp)
X =
[[[1 5 3]
[2 6 1]
[0 4 7]]
[[0 8 6]
[4 3 0]
[4 6 8]]]
Xp =
[[[0. 1. 5. 3. 0. 0.]
[0. 2. 6. 1. 0. 0.]
[0. 0. 4. 7. 0. 0.]
[0. 0. 0. 0. 0. 0.]]
[[0. 0. 8. 6. 0. 0.]
[0. 4. 3. 0. 0. 0.]
[0. 4. 6. 8. 0. 0.]
[0. 0. 0. 0. 0. 0.]]]
We see that the right of the input is padded.
Test the value of \(p\) as integer (\(p=1\))
import numpy as np
np.random.seed(10)
X = np.random.randint(0,10, size=(2,3,3))
X[0,:,:] = np.array([[1, 5, 3],
[2, 6, 1],
[0, 4, 7]])
K = np.array([[1, -1],
[2, 0]])
s = (2,2) # strides along height and width
print('X = \n\n', X, '\n')
Xp = pad_input2D_batch(X, K, s, p=1)
print('Xp = \n\n', Xp)
X =
[[[1 5 3]
[2 6 1]
[0 4 7]]
[[0 8 6]
[4 3 0]
[4 6 8]]]
Xp =
[[[0. 0. 0. 0. 0.]
[0. 1. 5. 3. 0.]
[0. 2. 6. 1. 0.]
[0. 0. 4. 7. 0.]
[0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0.]
[0. 0. 8. 6. 0.]
[0. 4. 3. 0. 0.]
[0. 4. 6. 8. 0.]
[0. 0. 0. 0. 0.]]]
Next the function conv2d_batch(X,K,s,p) performs convolution between input \(X\) (containing batch but no channels) and Kernel \(K\) and returns the convolved matrix \(Z\) (Output).
def conv2d_batch(X, K, s=(1,1), p='valid'):
# padding
Xp = pad_input2D_batch(X, K, s, p=p)
print('Xp = \n\n', Xp, '\n')
m, Nh, Nw = Xp.shape
Kh, Kw = K.shape
sh, sw = s # strides along height and width
Oh = (Nh-Kh)//sh + 1
Ow = (Nw-Kw)//sw + 1
strides = (Nh*Nw, sh*Nw, sw, Nw, 1)
strides = tuple(i * Xp.itemsize for i in strides)
subM = np.lib.stride_tricks.as_strided(Xp, shape=(m, Oh, Ow, Kh, Kw),
strides=strides)
return np.einsum('kl,mijkl->mij', K, subM)
Test with p='same'
np.random.seed(10)
X = np.random.randint(0,10, size=(2,3,3))
X[0,:,:] = np.array([[1, 5, 3],
[2, 6, 1],
[0, 4, 7]])
K = np.array([[1, -1],
[2, 0]])
s = (2,2)
print('X = \n\n', X, '\n')
print('K = \n\n', K, '\n')
Z = conv2d_batch(X, K, s, p='same')
print('Z = \n\n', Z)
X =
[[[1 5 3]
[2 6 1]
[0 4 7]]
[[0 8 6]
[4 3 0]
[4 6 8]]]
K =
[[ 1 -1]
[ 2 0]]
Xp =
[[[0. 0. 0. 0. 0. 0.]
[0. 1. 5. 3. 0. 0.]
[0. 2. 6. 1. 0. 0.]
[0. 0. 4. 7. 0. 0.]
[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0. 0.]
[0. 0. 8. 6. 0. 0.]
[0. 4. 3. 0. 0. 0.]
[0. 4. 6. 8. 0. 0.]
[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]]]
Z =
[[[ 0. 10. 0.]
[-2. 13. 0.]
[ 0. 0. 0.]]
[[ 0. 16. 0.]
[-4. 15. 0.]
[ 0. 0. 0.]]]
Input with batch of images (with channels)#
Next we will also include channels to image as Input
A batch of images (with channels) as input of shape \((m, N_c, N_h, N_w)\) is used.
Note: See how the depth of the Kernel is same as the number of channels (one 2D kernel for each channel). Till now we only have 1 Kernel, in the next section we will also add multiple Kernels.
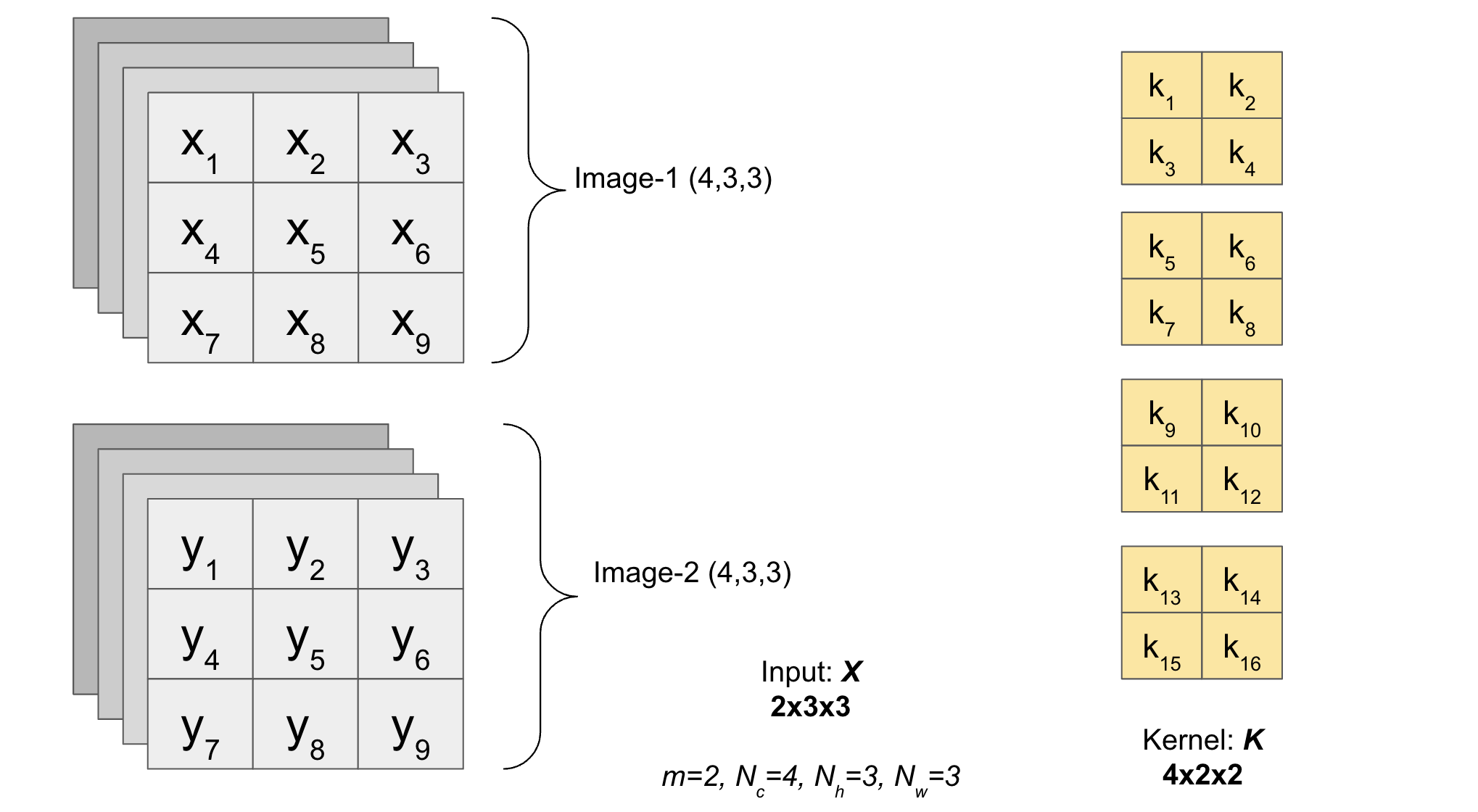
The function pad_input2D_with_channels_batch(X,K,s,p) performs padding on input \(X\) (with channels) and returns the padded matrix.
def pad_input2D_with_channels_batch(X, K, s, p='valid'):
if type(p)==int:
m, Nc, Nh, Nw = X.shape
pt, pb = p, p
pl, pr = p, p
elif p=='valid':
m, Nc, Nh, Nw = X.shape
pt, pb = 0, 0
pl, pr = 0, 0
elif p=='same':
m, Nc, Nh, Nw = X.shape
Kc, Kh, Kw = K.shape
sh, sw = s
ph = (sh-1)*Nh + Kh - sh
pw = (sw-1)*Nw + Kw - sw
pt, pb = ph//2, (ph+1)//2
pl, pr = pw//2, (pw+1)//2
else:
raise ValueError("Incorrect padding type. Allowed types are only 'same' or 'valid'.")
zeros_r = np.zeros((m, Nc, Nh, pr))
zeros_l = np.zeros((m, Nc, Nh, pl))
zeros_t = np.zeros((m, Nc, pt, Nw+pl+pr))
zeros_b = np.zeros((m, Nc, pb, Nw+pl+pr))
Xp = np.concatenate((X, zeros_r), axis=3)
Xp = np.concatenate((zeros_l, Xp), axis=3)
Xp = np.concatenate((zeros_t, Xp), axis=2)
Xp = np.concatenate((Xp, zeros_b), axis=2)
return Xp
Test \(p=1\)
import numpy as np
np.random.seed(10)
X = np.random.randint(0,10, size=(2,2,3,3))
# different K for each channel
K = np.random.randint(0,10, size=(2,2,2))
s = (2,2) # strides along height and width
print('X = \n\n', X, '\n')
Xp = pad_input2D_with_channels_batch(X, K, s, p=1)
print('Xp = \n\n', Xp)
X =
[[[[9 4 0]
[1 9 0]
[1 8 9]]
[[0 8 6]
[4 3 0]
[4 6 8]]]
[[[1 8 4]
[1 3 6]
[5 3 9]]
[[6 9 1]
[9 4 2]
[6 7 8]]]]
Xp =
[[[[0. 0. 0. 0. 0.]
[0. 9. 4. 0. 0.]
[0. 1. 9. 0. 0.]
[0. 1. 8. 9. 0.]
[0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0.]
[0. 0. 8. 6. 0.]
[0. 4. 3. 0. 0.]
[0. 4. 6. 8. 0.]
[0. 0. 0. 0. 0.]]]
[[[0. 0. 0. 0. 0.]
[0. 1. 8. 4. 0.]
[0. 1. 3. 6. 0.]
[0. 5. 3. 9. 0.]
[0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0.]
[0. 6. 9. 1. 0.]
[0. 9. 4. 2. 0.]
[0. 6. 7. 8. 0.]
[0. 0. 0. 0. 0.]]]]
Next the function conv2d_with_channels_batch(X,K,s,p) performs convolution between input \(X\) (containing batch and channels) and Kernel \(K\) and returns the convolved matrix \(Z\) (Output).
Note: We sum the values of the convolution obtained across channels.
def conv2d_with_channels_batch(X, K, s, p='valid'):
# padding
Xp = pad_input2D_with_channels_batch(X, K, s, p=p)
print('Xp = \n\n', Xp, '\n')
m, Nc, Nh, Nw = Xp.shape
Kc, Kh, Kw = K.shape
sh, sw = s # strides along height and width
Oh = (Nh-Kh)//sh + 1
Ow = (Nw-Kw)//sw + 1
strides = (Nc*Nh*Nw, Nw*Nh, Nw*sh, sw, Nw, 1)
strides = tuple(i * Xp.itemsize for i in strides)
subM = np.lib.stride_tricks.as_strided(Xp, shape=(m, Nc, Oh, Ow, Kh, Kw),
strides=strides)
return np.einsum('ckl,mcijkl->mij', K, subM)
Test p="same"
import numpy as np
np.random.seed(10)
X = np.random.randint(0,10, size=(2,2,3,3))
# different K for each channel
K = np.random.randint(0,10, size=(2,2,2))
s = (2,2) # strides along height and width
print('X = \n\n', X, '\n')
print('K = \n\n', K, '\n')
Z = conv2d_with_channels_batch(X, K, s, p='same')
print('Z = \n\n', Z)
X =
[[[[9 4 0]
[1 9 0]
[1 8 9]]
[[0 8 6]
[4 3 0]
[4 6 8]]]
[[[1 8 4]
[1 3 6]
[5 3 9]]
[[6 9 1]
[9 4 2]
[6 7 8]]]]
K =
[[[8 9]
[2 0]]
[[6 7]
[8 1]]]
Xp =
[[[[0. 0. 0. 0. 0. 0.]
[0. 9. 4. 0. 0. 0.]
[0. 1. 9. 0. 0. 0.]
[0. 1. 8. 9. 0. 0.]
[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0. 0.]
[0. 0. 8. 6. 0. 0.]
[0. 4. 3. 0. 0. 0.]
[0. 4. 6. 8. 0. 0.]
[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]]]
[[[0. 0. 0. 0. 0. 0.]
[0. 1. 8. 4. 0. 0.]
[0. 1. 3. 6. 0. 0.]
[0. 5. 3. 9. 0. 0.]
[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0. 0.]
[0. 6. 9. 1. 0. 0.]
[0. 9. 4. 2. 0. 0.]
[0. 6. 7. 8. 0. 0.]
[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]]]]
Z =
[[[ 0. 78. 0.]
[ 41. 162. 0.]
[ 0. 0. 0.]]
[[ 6. 89. 0.]
[ 78. 186. 0.]
[ 0. 0. 0.]]]
Input with batch of images (with channels) and multiple filters#
Finally we will also include multiple Kernels (or filters) - Most general 2D padding and convolution
The shape of Kernel will be \((F, K_c, K_h, K_w)\) where \(F\) is the total number of filters.
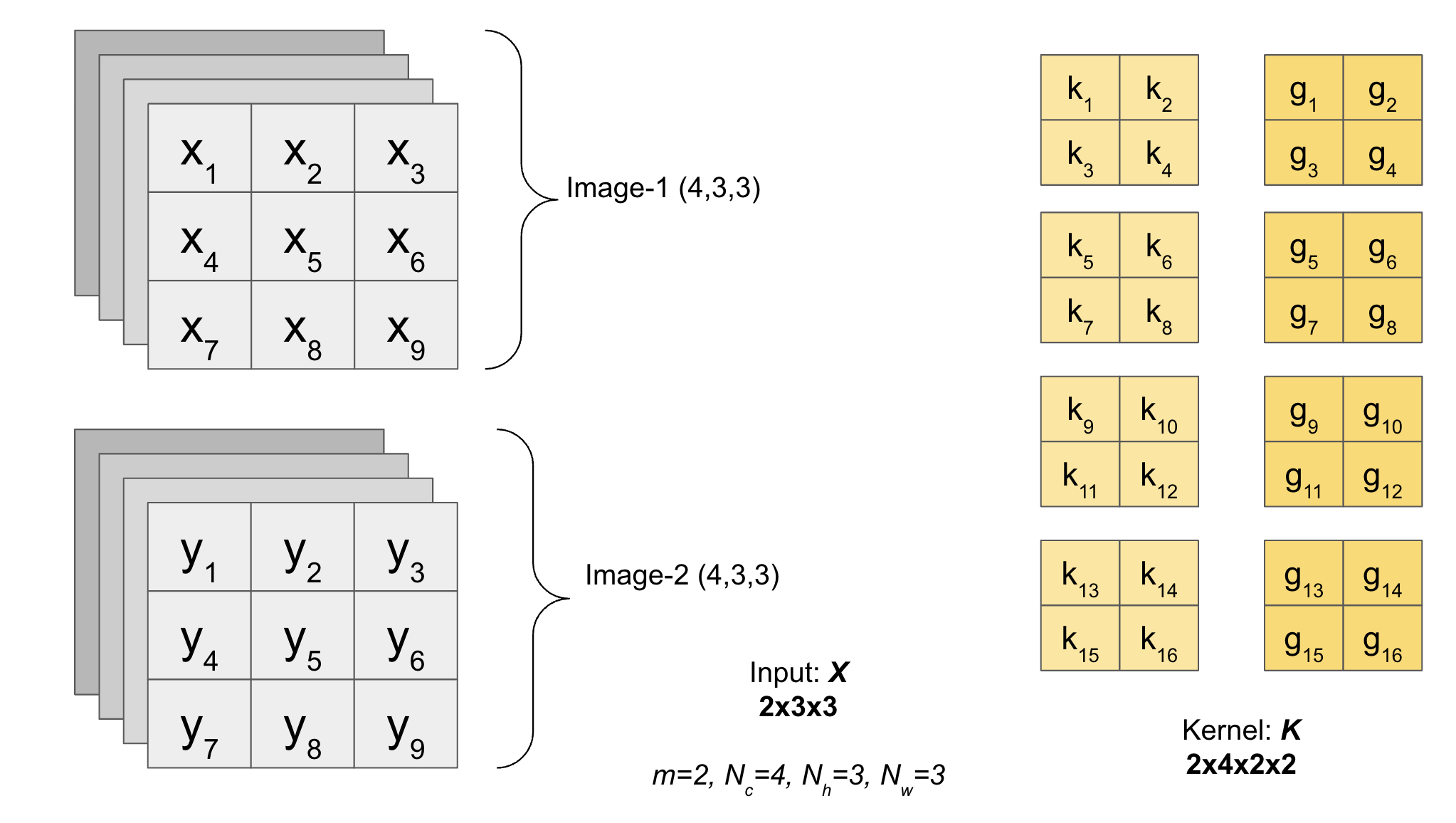
The function pad_input2D_with_channels_batch_and_many_filters(X,K,s,p) performs padding on input \(X\) and returns the padded matrix.
def pad_input2D_with_channels_batch_and_many_filters(X, K, s, p='valid'):
if type(p)==int:
m, Nc, Nh, Nw = X.shape
pt, pb = p, p
pl, pr = p, p
elif p=='valid':
m, Nc, Nh, Nw = X.shape
pt, pb = 0, 0
pl, pr = 0, 0
elif p=='same':
m, Nc, Nh, Nw = X.shape
F, Kc, Kh, Kw = K.shape # F = number of filters
sh, sw = s
ph = (sh-1)*Nh + Kh - sh
pw = (sw-1)*Nw + Kw - sw
pt, pb = ph//2, (ph+1)//2
pl, pr = pw//2, (pw+1)//2
else:
raise ValueError("Incorrect padding type. Allowed types are only 'same' or 'valid' or an integer.")
zeros_r = np.zeros((m, Nc, Nh, pr))
zeros_l = np.zeros((m, Nc, Nh, pl))
zeros_t = np.zeros((m, Nc, pt, Nw+pl+pr))
zeros_b = np.zeros((m, Nc, pb, Nw+pl+pr))
Xp = np.concatenate((X, zeros_r), axis=3)
Xp = np.concatenate((zeros_l, Xp), axis=3)
Xp = np.concatenate((zeros_t, Xp), axis=2)
Xp = np.concatenate((Xp, zeros_b), axis=2)
return Xp
Test p=1
import numpy as np
np.random.seed(10)
X = np.random.randint(0,10, size=(2,3,3,3))
# different Kernel for each channel and many such filters
K = np.random.randint(0,10, size=(2,3,2,2))
s = (1,2) # strides along height and width
print('X = \n\n', X, '\n')
print('K = \n\n', K, '\n')
Xp = pad_input2D_with_channels_batch_and_many_filters(X, K, s, p=1)
print('Xp = \n\n', Xp)
X =
[[[[9 4 0]
[1 9 0]
[1 8 9]]
[[0 8 6]
[4 3 0]
[4 6 8]]
[[1 8 4]
[1 3 6]
[5 3 9]]]
[[[6 9 1]
[9 4 2]
[6 7 8]]
[[8 9 2]
[0 6 7]
[8 1 7]]
[[1 4 0]
[8 5 4]
[7 8 8]]]]
K =
[[[[2 6]
[2 8]]
[[8 6]
[6 5]]
[[6 0]
[0 6]]]
[[[9 1]
[8 9]]
[[1 2]
[8 9]]
[[9 5]
[0 2]]]]
Xp =
[[[[0. 0. 0. 0. 0.]
[0. 9. 4. 0. 0.]
[0. 1. 9. 0. 0.]
[0. 1. 8. 9. 0.]
[0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0.]
[0. 0. 8. 6. 0.]
[0. 4. 3. 0. 0.]
[0. 4. 6. 8. 0.]
[0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0.]
[0. 1. 8. 4. 0.]
[0. 1. 3. 6. 0.]
[0. 5. 3. 9. 0.]
[0. 0. 0. 0. 0.]]]
[[[0. 0. 0. 0. 0.]
[0. 6. 9. 1. 0.]
[0. 9. 4. 2. 0.]
[0. 6. 7. 8. 0.]
[0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0.]
[0. 8. 9. 2. 0.]
[0. 0. 6. 7. 0.]
[0. 8. 1. 7. 0.]
[0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0.]
[0. 1. 4. 0. 0.]
[0. 8. 5. 4. 0.]
[0. 7. 8. 8. 0.]
[0. 0. 0. 0. 0.]]]]
Finally the function conv2d_with_channels_batch_and_many_filters(X,K,s,p,mode) performs convolution between input \(X\) (with batch and channels) and Kernel \(K\) (many such kernels) and returns the convolved matrix \(Z\) (Output).
Notice since this is the most general model that can be developed using the parameters we have defined till now, so there is another arguement added to this function mode which will either be forward or backward depending on the type of propagation we will be performing and notice how only the last line of the code changes (which includes only an extra if else statement)
def conv2d_with_channels_batch_and_many_filters(X, K, s, p='valid', mode='front'):
# padding
Xp = pad_input2D_with_channels_batch_and_many_filters(X, K, s, p=p)
print("Xp = \n\n", Xp, '\n')
m, Nc, Nh, Nw = Xp.shape
F, Kc, Kh, Kw = K.shape # F = number of filters
sh, sw = s # strides along height and width
Oh = (Nh-Kh)//sh + 1
Ow = (Nw-Kw)//sw + 1
strides = (Nc*Nh*Nw, Nw*Nh, Nw*sh, sw, Nw, 1)
strides = tuple(i * Xp.itemsize for i in strides)
subM = np.lib.stride_tricks.as_strided(Xp, shape=(m, Nc, Oh, Ow, Kh, Kw),
strides=strides)
if mode=='front':
return np.einsum('fckl,mcijkl->mfij', K, subM)
elif mode=='back':
return np.einsum('fdkl,mcijkl->mdij', K, subM)
Test p="same"
np.random.seed(10)
X = np.random.randint(0,10, size=(2,2,3,3))
# different Kernel for each channel and many such filters
K = np.random.randint(0,10, size=(2,2,2,2))
s = (2,2)
print('X = \n\n', X, '\n')
print('K = \n\n', K, '\n')
Z = conv2d_with_channels_batch_and_many_filters(X, K, s, p='same')
print('Z = \n\n', Z, '\n')
X =
[[[[9 4 0]
[1 9 0]
[1 8 9]]
[[0 8 6]
[4 3 0]
[4 6 8]]]
[[[1 8 4]
[1 3 6]
[5 3 9]]
[[6 9 1]
[9 4 2]
[6 7 8]]]]
K =
[[[[8 9]
[2 0]]
[[6 7]
[8 1]]]
[[[7 1]
[4 0]]
[[8 5]
[4 7]]]]
Xp =
[[[[0. 0. 0. 0. 0. 0.]
[0. 9. 4. 0. 0. 0.]
[0. 1. 9. 0. 0. 0.]
[0. 1. 8. 9. 0. 0.]
[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0. 0.]
[0. 0. 8. 6. 0. 0.]
[0. 4. 3. 0. 0. 0.]
[0. 4. 6. 8. 0. 0.]
[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]]]
[[[0. 0. 0. 0. 0. 0.]
[0. 1. 8. 4. 0. 0.]
[0. 1. 3. 6. 0. 0.]
[0. 5. 3. 9. 0. 0.]
[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0. 0.]
[0. 6. 9. 1. 0. 0.]
[0. 9. 4. 2. 0. 0.]
[0. 6. 7. 8. 0. 0.]
[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]]]]
Z =
[[[[ 0. 78. 0.]
[ 41. 162. 0.]
[ 0. 0. 0.]]
[[ 0. 90. 0.]
[ 49. 199. 0.]
[ 0. 0. 0.]]]
[[[ 6. 89. 0.]
[ 78. 186. 0.]
[ 0. 0. 0.]]
[[ 42. 75. 0.]
[ 88. 165. 0.]
[ 0. 0. 0.]]]]
Lastly we can add bias to the output tensor (depending on whether or not we want to add bias to the layer)


