2.10. Dropout regularization#

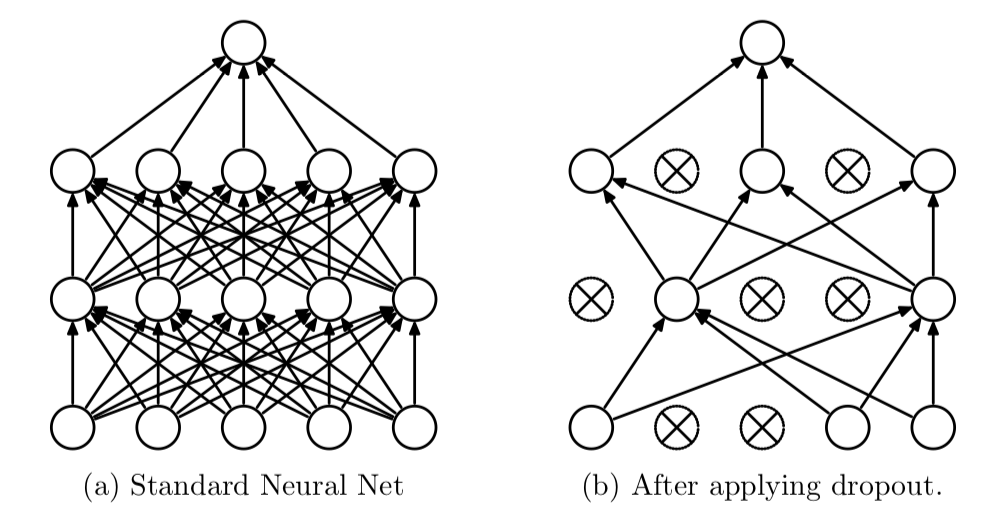
The term dropout refers to randomly dropping out the neurons in a neural network (as seen in the figure below). At each training stage, individual neurons are either dropped out of the net with probability \(p\) or kept with probability \(1-p\), so that a reduced network is left. In testing phase, the entire network is considered and each activation is reduced by a factor \(p\).

Dropout is an approach to regularization in neural networks which helps reducing interdependent learning amongst the neurons.

Dropout is effective especially when your network is very big or when you train for a very long time, both of which put a network at a higher risk of overfitting.

When you have very large training data sets, the utility of regularization techniques, including dropout, declines because the network has more data available to learn to generalize better.

Forward pass#

Without dropout, the feed forward operation on layer \(l\) (link to previous chapter) is:

\[ z_l = a_{l-1}W_l + b_l^T \]
\[ a_l = f_l(z_l) \]

When dropout is on, the equations become as follows:

\[ r_{l-1} \sim \text{Bernoulli(p)} \]
\[ \tilde{a}_{l-1} = r_{l-1} \odot a_{l-1} \]
\[ z_l = \tilde{a}_{l-1} W_l + b_l^T \]
\[ a_l = f_l(z_l) \]

Thus when the output of the neuron is scaled to 0 (using Bernoulli), it does not contribute any further during both forward and backward pass, which is essentially dropout.

During training phase, we trained the network with only a subset of the neurons. So during testing, we have to scale the output activations by factor of \(p\), which means we have to modify the network during test phase.

A simpler and commonly used alternative called Inverted Dropout scales the output activation during training phase by \(\frac{1}{p}\) so that we can leave the network during testing phase untouched.

The code for the same is fairly simple:

mask represents: \(r_{l-1}\)

out represents: \(\tilde{a}_{l-1}\)

t represents: Any input, here \(a_{l-1}\)

# create a mask of bernoulli variables and scale it by 1/p
# save it for backward pass
mask = (np.random.rand(*t.shape) < p) / p 
out = t * mask

Backpropagation#

Back propagation on layer \(l\) (link to previous chapter) is:

\[ \frac{\partial J(W, b)}{\partial \tilde{a}_{l-1}} = \delta_{l} W_{l}^T \]
\[ \frac{\partial J(W, b)}{\partial a_{l-1}} = \frac{\partial J(W, b)}{\partial \tilde{a}_{l-1}} \odot \frac{\partial \tilde{a}_{l-1}}{\partial a_{l-1}} \]
\[ \frac{\partial J(W, b)}{\partial a_{l-1}} = \frac{\partial J(W, b)}{\partial \tilde{a}_{l-1}} \odot r_{l-1} \]

Thats it!

dout represents: \(\frac{\partial J(W, b)}{\partial \tilde{a}_{l-1}}\)

dt represents: \(\frac{\partial J(W, b)}{\partial a_{l-1}}\)

# mask (saved during forward pass)
dt = dout * mask