3.2.4. Pooling layers
Contents
3.2.4. Pooling layers#
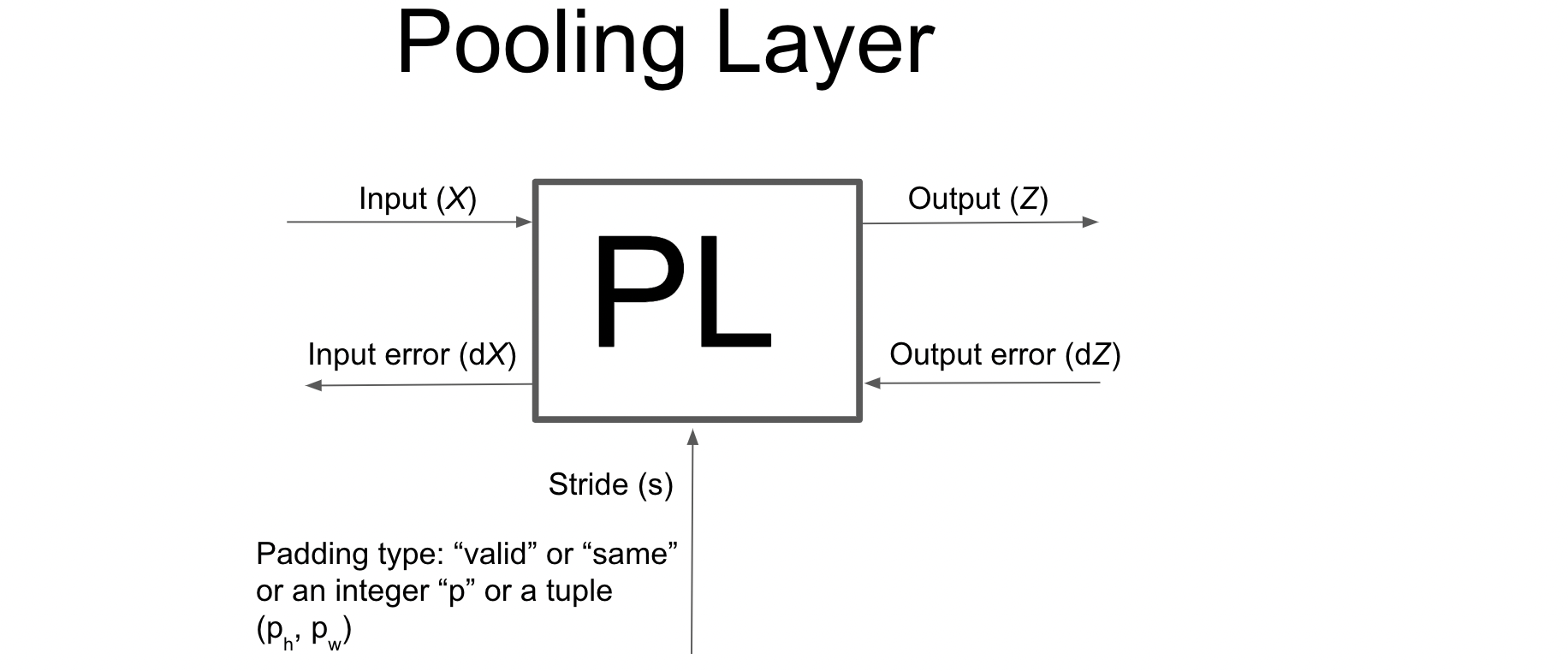
A major problem with convolutional layer is that the feature map (output) produced by the convolution between input and kernel is translation variant (that is location-dependent).
This means that if an object in an image has shifted a bit it might not be recognizable by the convolutional layer. So, it means that the feature map (output) records the precise positions of features in the input.
Therefore we want a layer which can take as input this feature map (output from convolution) and make it translation invariant (which means location of the feature should not matter). This is done by a pooling layer.
How does Pooling work?#
We select a Kernel and slide it over the feature map (output from the preceding convolution layer after activation is applied) and based on the type of pooling operation we’ve selected, the pooling kernel calculates an output.
The most commonly used Kernel size is \((2,2)\) along with a stride of 2.
Max Pooling#
In max pooling, the filter simply selects the maximum pixel value in the receptive field. From the below gif, we see that the kernel is selecting only the maximum value from the receptive field (like in the first slot, we have 4 pixels in the field with values 1, 5, 2, and 6, and we select 6).

Average Pooling#
In average pooling, the filter simply selects the average value of all the pixels in the receptive field.

Forward Propagation for Pooling layer#
Let us write the python code (using only numpy) to implement forward propagation in pooling layer!
Simple Input (no channels and batch)#
We will start with a simple Input (with no channels and batch) of shape \((N_h, N_w)\) and then progress further.

The function pad_input2D(X,K,s,p) performs padding on input \(X\) (with no channels and batch) and returns the padded matrix.
def pad_input2D(X, K=None, s=(1,1), p='valid', K_size=None):
if type(p)==int:
Nh, Nw = X.shape
pt, pb = p, p
pl, pr = p, p
if type(p)==tuple:
Nh, Nw = X.shape
ph,pw = p
pt, pb = ph//2, (ph+1)//2
pl, pr = pw//2, (pw+1)//2
elif p=='valid':
Nh, Nw = X.shape
pt, pb = 0, 0
pl, pr = 0, 0
elif p=='same':
Nh, Nw = X.shape
if K is not None:
Kh, Kw = K.shape
else:
Kh, Kw = K_size
sh, sw = s
ph = (sh-1)*Nh + Kh - sh
pw = (sw-1)*Nw + Kw - sw
pt, pb = ph//2, (ph+1)//2
pl, pr = pw//2, (pw+1)//2
else:
raise ValueError("Incorrect padding type. Allowed types are only 'same' or 'valid' or an integer.")
Xp = np.vstack((np.zeros((pt, Nw)), X))
Xp = np.vstack((Xp, np.zeros((pb, Nw))))
Xp = np.hstack((np.zeros((Nh+pt+pb, pl)), Xp))
Xp = np.hstack((Xp, np.zeros((Nh+pt+pb, pr))))
return Xp
The function pooling2d(X, pool_size, s, p, pool_type) performs max/mean pooling on a 2d array using numpy.
So, the idea is to create a sub-matrices of the input using the given kernel size and stride (with the help of as_stride() of numpy) and then simply take the maximum along the height and width axes.
Note: The main benefit of using this method is that it can be extended for input with channels (depth) and batches as well!
def pooling2d(X, pool_size=(2,2), s=(2,2), p='valid', pool_type='max'):
# padding
Xp = pad_input2D(X, s=s, p=p, K_size=pool_size)
print('Xp (padded X)' + ' for padding=' + str(p) + ' = \n\n', Xp, '\n')
Nh, Nw = Xp.shape
sh, sw = s # strides along height and width
Kh, Kw = pool_size
Oh = (Nh-Kh)//sh + 1
Ow = (Nw-Kw)//sw + 1
strides = (sh*Nw, sw, Nw, 1)
strides = tuple(i * Xp.itemsize for i in strides)
subM = np.lib.stride_tricks.as_strided(Xp, shape=(Oh, Ow, Kh, Kw),
strides=strides)
if pool_type=='max':
return np.max(subM, axis=(-2,-1)) # maximum along height and width
elif pool_type=='mean':
return np.mean(subM, axis=(-2,-1))
else:
raise ValueError("Allowed pool types are only 'max' or 'mean'.")
Try pool_type="max"
import numpy as np
np.random.seed(10)
X = np.array([[1,5,3,-3],
[2,6,-1,1],
[0,4,7,2],
[11,-5,8,6]])
pool_size = (2,2) # Kernel size
s = (2,2) # strides along height and width
print('X = \n\n', X, '\n')
Z = pooling2d(X, pool_size, s, p='same', pool_type='max')
print('Z = \n\n', Z, '\n')
X =
[[ 1 5 3 -3]
[ 2 6 -1 1]
[ 0 4 7 2]
[11 -5 8 6]]
Xp (padded X) for padding=same =
[[ 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 1. 5. 3. -3. 0. 0.]
[ 0. 0. 2. 6. -1. 1. 0. 0.]
[ 0. 0. 0. 4. 7. 2. 0. 0.]
[ 0. 0. 11. -5. 8. 6. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0.]]
Z =
[[ 0. 0. 0. 0.]
[ 0. 6. 3. 0.]
[ 0. 11. 8. 0.]
[ 0. 0. 0. 0.]]
Try pool_type="mean"
import numpy as np
np.random.seed(10)
X = np.array([[1,5,3,-3],
[2,6,-1,1],
[0,4,7,2],
[11,-5,8,7]])
pool_size = (2,2) # Kernel size
s = (2,2) # strides along height and width
print('X = \n\n', X, '\n')
Z = pooling2d(X, pool_size, s, p='same', pool_type='mean')
print('Z = \n\n', Z, '\n')
X =
[[ 1 5 3 -3]
[ 2 6 -1 1]
[ 0 4 7 2]
[11 -5 8 7]]
Xp (padded X) for padding=same =
[[ 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 1. 5. 3. -3. 0. 0.]
[ 0. 0. 2. 6. -1. 1. 0. 0.]
[ 0. 0. 0. 4. 7. 2. 0. 0.]
[ 0. 0. 11. -5. 8. 7. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0.]]
Z =
[[0. 0. 0. 0. ]
[0. 3.5 0. 0. ]
[0. 2.5 6. 0. ]
[0. 0. 0. 0. ]]
It worked like a charm! Let us now extend the same using input (with channels or depth and batches)
Input with batch of images (with channels)#
Next we will also include channels to image as Input
A batch of images (with channels) as input of shape \((m, N_c, N_h, N_w)\) is used.
Note: See how the depth of the pool is same as the number of channels (one 2D pool for each channel).
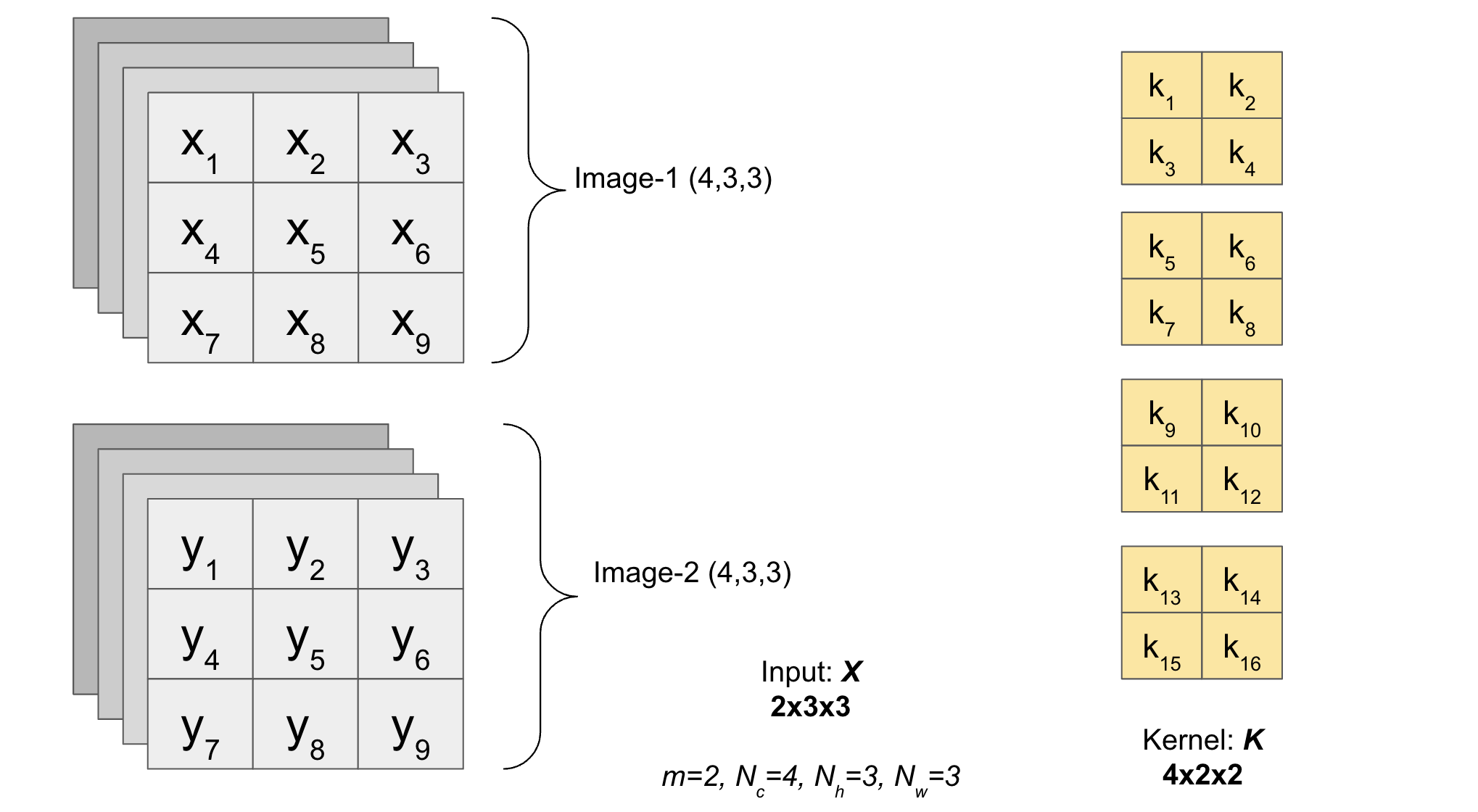
The function pad_input2D_with_channels_batch(X,K,s,p) performs padding on input \(X\) (with channels) and returns the padded matrix.
def pad_input2D_with_channels_batch(X, K=None, s=(1,1), p='valid', K_size=None):
if type(p)==int:
m, Nc, Nh, Nw = X.shape
pt, pb = p, p
pl, pr = p, p
if type(p)==tuple:
m, Nc, Nh, Nw = X.shape
ph, pw = p
pt, pb = ph//2, (ph+1)//2
pl, pr = pw//2, (pw+1)//2
elif p=='valid':
m, Nc, Nh, Nw = X.shape
pt, pb = 0, 0
pl, pr = 0, 0
elif p=='same':
m, Nc, Nh, Nw = X.shape
if K is not None:
Kc, Kh, Kw = K.shape
else:
Kh, Kw = K_size
sh, sw = s
ph = (sh-1)*Nh + Kh - sh
pw = (sw-1)*Nw + Kw - sw
pt, pb = ph//2, (ph+1)//2
pl, pr = pw//2, (pw+1)//2
else:
raise ValueError("Incorrect padding type. Allowed types are only 'same' or 'valid'.")
zeros_r = np.zeros((m, Nc, Nh, pr))
zeros_l = np.zeros((m, Nc, Nh, pl))
zeros_t = np.zeros((m, Nc, pt, Nw+pl+pr))
zeros_b = np.zeros((m, Nc, pb, Nw+pl+pr))
Xp = np.concatenate((X, zeros_r), axis=3)
Xp = np.concatenate((zeros_l, Xp), axis=3)
Xp = np.concatenate((zeros_t, Xp), axis=2)
Xp = np.concatenate((Xp, zeros_b), axis=2)
return Xp
def pooling2d_with_channels_batch(X, pool_size=(2,2), s=(2,2), p='valid', pool_type='max'):
# padding
Xp = pad_input2D_with_channels_batch(X, s=s, p=p, K_size=pool_size)
print('Xp (padded X)' + ' for padding=' + str(p) + ' = \n\n', Xp, '\n')
m, Nc, Nh, Nw = Xp.shape
sh, sw = s # strides along height and width
Kh, Kw = pool_size
Oh = (Nh-Kh)//sh + 1
Ow = (Nw-Kw)//sw + 1
strides = (Nc*Nh*Nw, Nh*Nw, Nw*sh, sw, Nw, 1)
strides = tuple(i * Xp.itemsize for i in strides)
subM = np.lib.stride_tricks.as_strided(Xp, shape=(m, Nc, Oh, Ow, Kh, Kw),
strides=strides)
a = subM.reshape(-1,Kh*Kw)
idx = np.argmax(a, axis=1)
b = np.zeros(a.shape)
b[np.arange(b.shape[0]), idx] = 1
mask = b.reshape((m, Nc, Oh, Ow, Kh, Kw))
if pool_type=='max':
return np.max(subM, axis=(-2,-1)), mask, Xp # maximum along height and width of submatrix
elif pool_type=='mean':
return np.mean(subM, axis=(-2,-1)), mask, Xp
else:
raise ValueError("Allowed pool types are only 'max' or 'mean'.")
Try pool_type="max"
import numpy as np
np.random.seed(10)
X = np.random.randint(0,10, size=(2,2,3,3))
pool_size = (2,2) # Kernel size
s = (1,2) # strides along height and width
print('X = \n\n', X, '\n')
Z, mask, Xp = pooling2d_with_channels_batch(X, pool_size, s, p='same', pool_type='max')
print('Z = \n\n', Z, '\n')
X =
[[[[9 4 0]
[1 9 0]
[1 8 9]]
[[0 8 6]
[4 3 0]
[4 6 8]]]
[[[1 8 4]
[1 3 6]
[5 3 9]]
[[6 9 1]
[9 4 2]
[6 7 8]]]]
Xp (padded X) for padding=same =
[[[[0. 9. 4. 0. 0. 0.]
[0. 1. 9. 0. 0. 0.]
[0. 1. 8. 9. 0. 0.]
[0. 0. 0. 0. 0. 0.]]
[[0. 0. 8. 6. 0. 0.]
[0. 4. 3. 0. 0. 0.]
[0. 4. 6. 8. 0. 0.]
[0. 0. 0. 0. 0. 0.]]]
[[[0. 1. 8. 4. 0. 0.]
[0. 1. 3. 6. 0. 0.]
[0. 5. 3. 9. 0. 0.]
[0. 0. 0. 0. 0. 0.]]
[[0. 6. 9. 1. 0. 0.]
[0. 9. 4. 2. 0. 0.]
[0. 6. 7. 8. 0. 0.]
[0. 0. 0. 0. 0. 0.]]]]
Z =
[[[[9. 9. 0.]
[1. 9. 0.]
[1. 9. 0.]]
[[4. 8. 0.]
[4. 8. 0.]
[4. 8. 0.]]]
[[[1. 8. 0.]
[5. 9. 0.]
[5. 9. 0.]]
[[9. 9. 0.]
[9. 8. 0.]
[6. 8. 0.]]]]
Try pool_type="mean"
import numpy as np
np.random.seed(10)
X = np.random.randint(0,10, size=(2,2,3,3))
pool_size = (2,2) # Kernel size
s = (1,2) # strides along height and width
print('X = \n\n', X, '\n')
Z, mask, Xp = pooling2d_with_channels_batch(X, pool_size, s, p='same', pool_type='mean')
print('Z = \n\n', Z, '\n')
X =
[[[[9 4 0]
[1 9 0]
[1 8 9]]
[[0 8 6]
[4 3 0]
[4 6 8]]]
[[[1 8 4]
[1 3 6]
[5 3 9]]
[[6 9 1]
[9 4 2]
[6 7 8]]]]
Xp (padded X) for padding=same =
[[[[0. 9. 4. 0. 0. 0.]
[0. 1. 9. 0. 0. 0.]
[0. 1. 8. 9. 0. 0.]
[0. 0. 0. 0. 0. 0.]]
[[0. 0. 8. 6. 0. 0.]
[0. 4. 3. 0. 0. 0.]
[0. 4. 6. 8. 0. 0.]
[0. 0. 0. 0. 0. 0.]]]
[[[0. 1. 8. 4. 0. 0.]
[0. 1. 3. 6. 0. 0.]
[0. 5. 3. 9. 0. 0.]
[0. 0. 0. 0. 0. 0.]]
[[0. 6. 9. 1. 0. 0.]
[0. 9. 4. 2. 0. 0.]
[0. 6. 7. 8. 0. 0.]
[0. 0. 0. 0. 0. 0.]]]]
Z =
[[[[2.5 3.25 0. ]
[0.5 6.5 0. ]
[0.25 4.25 0. ]]
[[1. 4.25 0. ]
[2. 4.25 0. ]
[1. 3.5 0. ]]]
[[[0.5 5.25 0. ]
[1.5 5.25 0. ]
[1.25 3. 0. ]]
[[3.75 4. 0. ]
[3.75 5.25 0. ]
[1.5 3.75 0. ]]]]
Back Propagation for Pooling layer#
Now let us write the python code (using only numpy) to implement backpropagation in the pooling layer!
Maxpool#
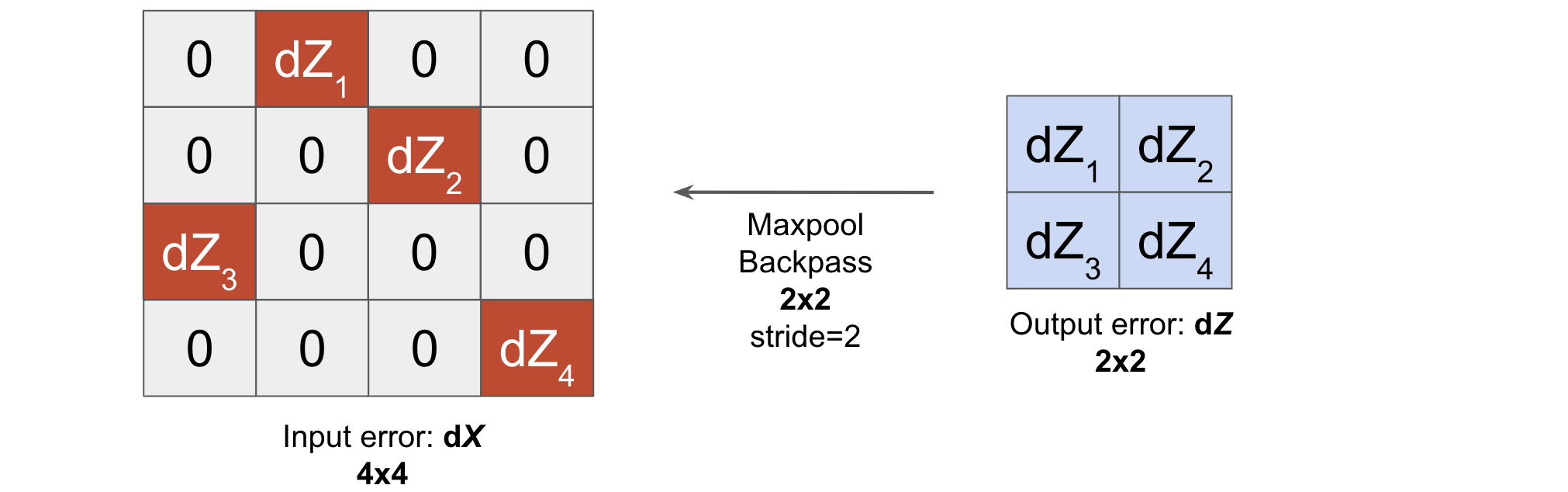
Suppose we have the following maxpool operation (forward) where the shaded pixels (in red) represents the maximum value of that receptive field.

Now, let the output error that we receive into this maxpool system be \(dZ\) such that:
The gradient of the error \(dX\) with respect to the input features is nonzero only if the input feature has the maximum value in the pooling kernel.
Using this strategy, we can compute the full backward pass (to compute \(dX\)) as follows:
# padding
import numpy as np
np.random.seed(10)
X = np.random.randint(0,10, size=(2,2,3,3))
pool_size = (2,2) # Kernel size
s = (1,2) # strides along height and width
Z, mask, Xp = pooling2d_with_channels_batch(X, pool_size, s, p='same', pool_type='mean')
Xp (padded X) for padding=same =
[[[[0. 9. 4. 0. 0. 0.]
[0. 1. 9. 0. 0. 0.]
[0. 1. 8. 9. 0. 0.]
[0. 0. 0. 0. 0. 0.]]
[[0. 0. 8. 6. 0. 0.]
[0. 4. 3. 0. 0. 0.]
[0. 4. 6. 8. 0. 0.]
[0. 0. 0. 0. 0. 0.]]]
[[[0. 1. 8. 4. 0. 0.]
[0. 1. 3. 6. 0. 0.]
[0. 5. 3. 9. 0. 0.]
[0. 0. 0. 0. 0. 0.]]
[[0. 6. 9. 1. 0. 0.]
[0. 9. 4. 2. 0. 0.]
[0. 6. 7. 8. 0. 0.]
[0. 0. 0. 0. 0. 0.]]]]
pooling2d_backwards_with_channels_batch(dZ, mask, X, pool_size) function implements the backpropagation in the maxpooling layer!
def pooling2d_max_backwards_with_channels_batch(dZ, mask, X, pool_size):
m, Nc, Nh, Nw = X.shape
Kh, Kw = pool_size
dA = np.einsum('i,ijk->ijk', dZ.reshape(-1), mask.reshape(-1,Kh,Kw)).reshape(mask.shape)
strides = (Nc*Nh*Nw, Nh*Nw, Nw, 1)
strides = tuple(i * X.itemsize for i in strides)
dX = np.lib.stride_tricks.as_strided(dA, X.shape, strides)
return dX
np.random.seed(10)
dZ = np.random.randint(-10, 10, Z.shape)
dXp = pooling2d_max_backwards_with_channels_batch(dZ, mask, Xp, pool_size)
dXp
array([[[[ 0., -1., 0., 0., 0., 0.],
[ -6., 0., 5., 0., 0., 0.],
[ 0., -10., 0., 0., 7., 0.],
[ 0., 0., 6., 0., 0., 0.]],
[[ 0., 7., 0., 0., 0., -2.],
[ 0., 0., -1., 0., 0., 0.],
[ 0., 0., 0., -10., 0., 0.],
[ 0., 0., -2., 0., 0., 0.]]],
[[[ 0., -6., 0., 0., 0., 0.],
[ 0., 9., 6., 0., 0., 0.],
[ 0., -6., 0., 0., 0., 5.],
[ 0., 0., 1., 0., 0., 0.]],
[[ 0., 1., 0., 0., -9., 0.],
[ 0., 0., -2., 0., 0., 0.],
[ 0., 0., 0., -6., 0., 0.],
[ 0., 4., 7., 0., 0., 0.]]]])
We need a small function such that we can extract the original input errors from the padding ones. This you can consider as backpropagation through padding operation
def padding2D_backwards_with_channels_batch(X, Xp, dXp):
m, Nc, Nh, Nw = Xp.shape
m, Nc, Nhx, Nwx = X.shape
ph = Nh - Nhx
pw = Nw - Nwx
pt, pb = ph//2, (ph+1)//2
pl, pr = pw//2, (pw+1)//2
dX = dXp[:, :, pt:pt+Nhx, pl:pl+Nwx]
return dX
dX = padding2D_backwards_with_channels_batch(X, Xp, dXp)
dX
array([[[[ -1., 0., 0.],
[ 0., 5., 0.],
[-10., 0., 0.]],
[[ 7., 0., 0.],
[ 0., -1., 0.],
[ 0., 0., -10.]]],
[[[ -6., 0., 0.],
[ 9., 6., 0.],
[ -6., 0., 0.]],
[[ 1., 0., 0.],
[ 0., -2., 0.],
[ 0., 0., -6.]]]])
Congrats! We have successfully calculated the gradients of the input \(dX\) for the maxpooling layer using only numpy (and no for loops)!
Average pool#
Now we will be writing the code for computing the gradient in case of average pooling. This code is also written using numpy and it is the most generalized code which runs without for loops and you will hardly find it anywhere on net!
I will not be going with the theoretical explaination but if you are interested you can visit this site.
def pooling2d_avg_backwards_with_channels_batch(dZ, s, X, pool_size):
m, Nc, Nh, Nw = X.shape
sh, sw = s
Kh, Kw = pool_size
dZp = np.kron(dZ, np.ones((Kh,Kw), dtype=dZ.dtype)) # similar to repelem in matlab
jh, jw = Kh-sh, Kw-sw # jump along height and width
if jw!=0:
L = dZp.shape[-1]-1
l1 = np.arange(sw, L)
l2 = np.arange(sw + jw, L + jw)
mask = np.tile([True]*jw + [False]*jw, len(l1)//jw).astype(bool)
r1 = l1[mask[:len(l1)]]
r2 = l2[mask[:len(l2)]]
dZp[:, :, :, r1] += dZp[:, :, :, r2]
dZp = np.delete(dZp, r2, axis=-1)
if jh!=0:
L = dZp.shape[-2]-1
l1 = np.arange(sh, L)
l2 = np.arange(sh + jh, L + jh)
mask = np.tile([True]*jh + [False]*jh, len(l1)//jh).astype(bool)
r1 = l1[mask[:len(l1)]]
r2 = l2[mask[:len(l2)]]
dZp[:, :, r1, :] += dZp[:, :, r2, :]
dZp = np.delete(dZp, r2, axis=-2)
pw = Nw - dZp.shape[-1]
ph = Nh - dZp.shape[-2]
dXp = pad_input2D_with_channels_batch(dZp, s=s, p=(ph, pw), K_size=pool_size)
return dXp / (Nh*Nw)
np.random.seed(10)
dZ = np.random.randint(-10, 10, Z.shape)
dXp = pooling2d_avg_backwards_with_channels_batch(dZ, s, Xp, pool_size)
dXp.shape
(2, 2, 4, 6)
dX = padding2D_backwards_with_channels_batch(X, Xp, dXp)
dX
array([[[[-0.04166667, -0.25 , -0.25 ],
[-0.45833333, 0.04166667, 0.04166667],
[-0.125 , 0.20833333, 0.20833333]],
[[-0.41666667, 0. , 0. ],
[-0.66666667, 0.375 , 0.375 ],
[-0.5 , 0.58333333, 0.58333333]]],
[[[ 0.04166667, -0.375 , -0.375 ],
[-0.20833333, -0.20833333, -0.20833333],
[ 0.125 , 0.29166667, 0.29166667]],
[[ 0.125 , 0.375 , 0.375 ],
[ 0.20833333, 0. , 0. ],
[ 0.41666667, -0.25 , -0.25 ]]]])


